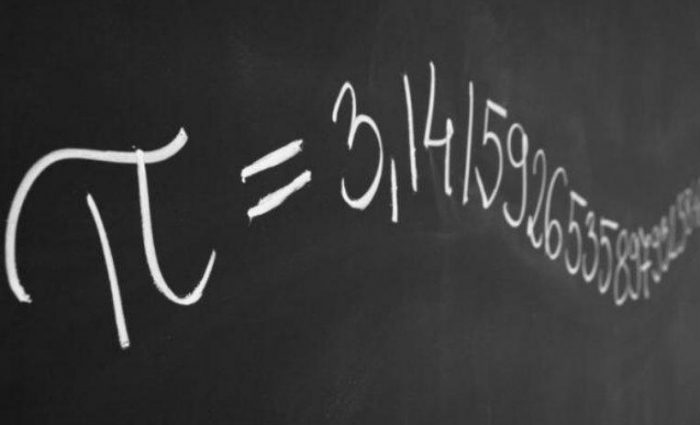¿Por qué los dígitos de PI son tan intrigantes y deben seguir siendo estudiados?

Hace un par de días (mes 3, día 14) se celebró en todo el mundo el “día de ’π’. Sin embargo, a diferencia de lo que ocurrió hace dos años –cuando se celebró el “gran día de π” (mes 3, día 14, año 15) sin que prácticamente nadie mencionara el tema–, esta vez la instancia generó una inusitada repercusión mediática. Para quienes practicamos la matemática, resulta a la vez inspirador y auspicioso constatar que la mayoría de los medios de prensa dedicaron al menos una nota al asunto. Lamentablemente, algunas de ellas tendieron a centrarse más bien en datos anecdóticos, que pueden llegar a parecer incluso como “simples pasatiempos freak” si son presentados sin mayor explicación. Tal es el caso, por ejemplo, del nuevo récord de almacenamiento digital de dígitos de π del suizo Peter Trueb (22.459.157.718.361 en total). Por esta razón, los comentarios de varios lectores de dichas columnas, que se preguntan –muchas veces despectivamente– por el interés de este tipo de “hazañas”, se hacen perfectamente entendibles.

Ahora bien, ¿por qué son tan interesantes los dígitos de π?

Recordemos que π corresponde al largo de una cuerda con forma de una circunferencia perfecta de diámetro 1 si la cortamos en un punto y la disponemos completamente estirada (link aquí). Se trata de un número irracional, es decir, un número cuya expresión decimal nunca desemboca en un patrón que se repite indefinidamente, como sí ocurre, por ejemplo, con 0,3333333333… o 5,718626262626262… Es por ello que, para trabajar con él en diversos campos tanto fundamentales como aplicados (matemática, física, ingeniería, astronomía, etc), suele recurrirse a aproximaciones, siendo 3,14 y 3,1415 las más conocidas. Para todos los efectos prácticos, una aproximación de una decena de decimales es ampliamente suficiente. ¿Por qué desgastarse entonces en calcular y almacenar 22.459.157.718.361 decimales?

Sucede que, hasta el día de hoy, aún no entendemos π del todo y, más ampliamente, aún no entendemos del todo los números. Para mostrar tan solo una de las interrogantes fundamentales que nos mueven, transcribo abajo una de las aproximaciones más interesantes de π:

π: 3.14159265358979323846264338327950…

El interés de esta radica en que se trata de la aproximación más corta en la que aparecen todos los dígitos del 0 al 9, siendo el 0 el último en aparecer. Surge entonces naturalmente una pregunta: ¿aparecerán infinitos dígitos 0 en la expresión decimal infinita de π ? ¿Aparecerán infinitos dígitos 1, 2, 3, etc.? Increíblemente, aún no tenemos respuesta para esto.

Se cree que en la expresión decimal de π no solo cada dígito tiene que estar incluido infinitas veces, sino que, además, cada uno de ellos tiene que aparecer “en la misma proporción”. Por ejemplo, entre las primeras diez millones cifras decimales de π , debiese haber alrededor de un millón de cifras 0, 1, 2, etc. Y tal es el caso, pues hasta este nivel de desarrollo aparecen exactamente:

999440   dígitos 0,

999333   dígitos 1,

1000306   dígitos 2,

999965   dígitos 3,

1001093   dígitos 4,

1000466   dígitos 5,

999337   dígitos 6,

1000206   dígitos 7,

999814   dígitos 8,

1000040   dígitos 9.

Pero no solo esto. Dada cualquier configuración finita de dígitos que se pueda imaginar, como por ejemplo 982637153904 o 58272635491010283, se cree que dicha configuración debe aparecer en la escritura de decimal de π, y que lo debe hacer infinitas veces (esto sin importar el largo de la configuración que se considere). Y algo así sería extraordinariamente interesante. Para vislumbrarlo, como simple ejercicio mental pensemos en que toda obra escrita de la humanidad puede ser codificada en dígitos, usando –por ejemplo– el 1 para la letra a, el 2 para la b, etc. De esta manera, cada obra literaria se torna equivalente a un gran número, es decir, a una configuración de dígitos. Pues bien, en la expresión decimal de π debiese haber copias de todos esos números: la poesía de Gabriela Mistral, las obras de Shakespeare, los cuentos de Borges y los chistes de Condorito, todos debieran estar codificados en π, y debiesen aparecer una infinidad de veces…

A los números que verifican la propiedad de hacer aparecer todas las configuraciones finitas de dígitos se les denomina “normales” (aunque, coincidirá usted en que bien podría denominárselos “borgianos”).

Paradojalmente, no es difícil establecer que “la gran mayoría” de los números son normales. Sin embargo, saber si números específicos lo son es una de las grandes preguntas abiertas de la aritmética. Y esto no es una exclusividad de π, pues se ignora la respuesta para números aún más sencillos, como la raíz cuadrada de 2 o el número de oro (aquel que aparece en el diseño de nuestra bandera de la independencia; link aquí). En esta expectación, contar con datos como los del último récord de almacenamiento de dígitos de π puede ser de gran ayuda. Por lo demás, constituye una muestra de cuán importante puede ser hoy en día el uso de computadores en la orientación de la investigación teórica.

Muy probablemente, cuando la interrogante de la “normalidad de π ” sea resuelta, la solución provendrá de la revelación de una instancia sobre la naturaleza íntima de los números que aún nos resulta desconocida. Esta tendrá, seguramente, amplias repercusiones en muchos contextos, pero nos es imposible imaginar exactamente qué nos deparará el camino para llegar a este descubrimiento. Y es así como suele operar la ciencia básica, la cual lleva implícita consigo una cuota de impredecibilidad abismante. A modo de ejemplo, nadie hubiese podido intuir la enorme revolución que constituirían la invención del cálculo diferencial o la relatividad en sus respectivas épocas.

En este contexto de incertidumbre, iniciativas como el concurso de infografías sobre π para estudiantes (divulgado por este medio hace algunos días, link aquí) son muy importantes. ¿Quién sabe? Tal vez el misterio de los números sea finalmente resuelto en un par de décadas por una niña o un niño que inició su carrera a través de este concurso…