La soledad de un nuevo número primo

La Soledad de los Números Primos es el título de la primera novela del joven autor italiano Paolo Giordano, quien además de escritor es doctor en física de la Universidad de Turín. Este certero y punzante relato sobre la soledad humana toma su nombre de un fenómeno que, desde tiempos remotos, ha sido fuente de investigación en matemática y es (y será por siempre) uno de los principales problemas de esta ciencia: la extraña y sorprendente distribución de los números primos.

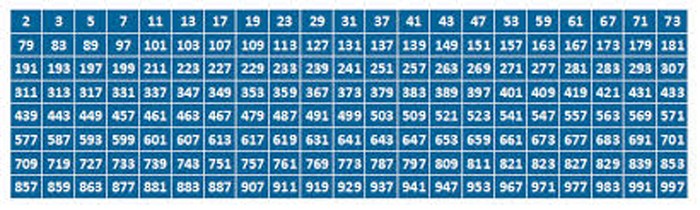
Recordemos primeramente que un número (entero y positivo) es “primo” si no puede ser expresado como producto de enteros mayores que 1. Así, 13 es primo, pero 15 no lo es, pues 15 = 3 x 5. La lista de los primeros primos empieza entonces con 2, 3, 5, 7, 11, 13, 17, 19, … Estos números son los “átomos” de la aritmética, pues a partir de ellos se puede obtener cualquier otro número por medio de multiplicaciones (recuerde la “factorización en números primos” aprendida en la escuela). De hecho, el nom-bre “primo” deriva de esto, pues se trata de los “números primarios”.

¿Cómo listar los números primos? El sabio helénico Eratóstenes ideó un proceso muy sencillo para descubrir sistemáticamente todos los primos: “Escriba todos los números (más bien, los que pueda) de manera ascendente a partir del 2 (que es el menor primo). A continuación, borre todos los números mayores que son múltiplos de 2, es decir, pares. El primer número que sobrevive en la lista es 3: este número es necesariamente primo. Ahora borre todos los múltiplos de 3 mayores que 3. Sobrevive entonces el próximo primo, el 5. Borre todos los múltiplos de 5 mayores que 5 y obtenga el 7… Con paciencia, irá descubriendo lentamente todos los primos”. Para una bonita animación explicativa de este proceso, vea https://en.wikipedia.org/wiki/Prime_number#/media/File:Sieve_of_Eratosthenes_animation.gif

¿Cuántos números primos hay? El proceso de Eratóstenes no responde a esta pregunta, pues se trata más bien de un método para detectar primos a medida que éstos aparecen. Hubo que esperar un tiempo hasta que otro sabio helénico, Euclides, diera con un argumento tan contundente como elegante para demostrar que la cantidad de primos es infinita: “Si se multiplican todos los números primos hallados hasta cierto momento y al resultado se le añade 1, entonces el número obtenido no puede ser dividido por ninguno de estos primos, por lo que debe existir al menos un primo más”.

Así, los números primos “son pocos, pero son”. De hecho, debiésemos esperar que los primos menores que 10ⁿ (el número formado por un dígito 1 seguido de n dígitos 0) sea algo así como 10ⁿ/n. Este hecho es una consecuencia del teorema de los números primos, una de las piezas más importantes de la teoría de números, la rama de la matemática que se ocupa de estos temas y que se conecta con otras líneas de estudio de mucha aplicación. Entre estas últimas destaca especialmente la criptografía, que es utilizada cotidianamente pues brinda el sustento teórico que permite la encriptación de datos, la cual nos da seguridad, por ejemplo, para realizar operaciones bancarias en internet. Aunque parezca sorprendente, ¡la dificultad para decodificar información de esta naturaleza de manera fraudulenta se debe al simple hecho de que es difícil escribir ciertos números como productos de primos!

Por razones un poco largas de explicar, una familia de primos particularmente interesante y fácil de trabajar es la de los números de Mersenne, constituida por los primos iguales a una potencia de 2 menos 1. La lista de los siete primeros primos de este tipo es:

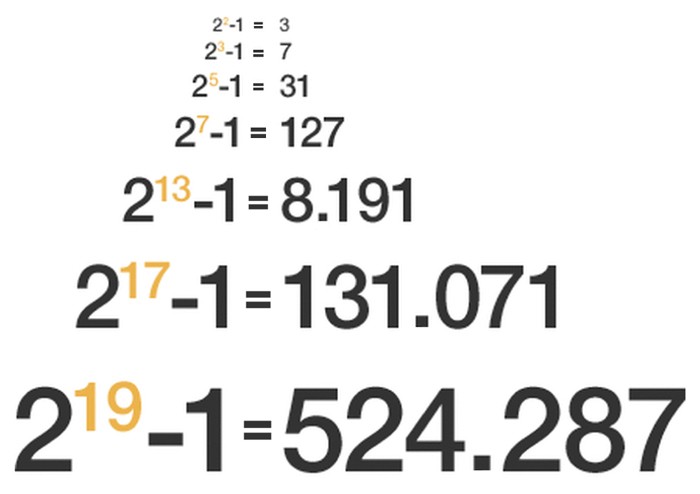
Hasta ahora, el número primo más grande conocido (descubierto en 2013) pertenecía a esta familia: 2^57.885.161 – 1. Su detección la había logrado un equipo de investigación en línea formado por voluntarios, el Great Prime Internet Research (fundado por George Woltman). Sin embargo, hace unos días, este mismo grupo anunció el descubrimiento de un nuevo primo del mismo tipo: 2^74.207.281 – 1. Este número, mayor que el anterior, consta de nada menos que de 22.338.618 dígitos. Para hacerse una idea de cómo se vería escrito, se puede visitar  https://www.youtube.com/watch?v=tlpYjrbujG0    

Si bien este hallazgo fue celebrado en el mundo entero –y ciertamente merece ser aplaudido-, es útil señalar que no se trata de un avance especialmente “importante” para la teoría. Contrariamente a lo que se suele pensar, la matemática no es una ciencia de cálculo, sino de comprensión. En este sentido, mucho más relevante que el descubrimiento de nuevos números primos es el estudio de la relaciones entre ellos: ¿qué tan regularmente aparecen estos números?, ¿por qué a veces tienden a desaparecer, para luego reaparecer en pares?, ¿cómo se combinan bajo operaciones distintas a la multiplicación?

Cada una de las preguntas anteriores se puede ejemplificar con descubrimientos relativamente recientes. Por ejemplo, hasta el día de hoy se des-conoce si existen infinitos primos para los cuales el número impar inmediatamente siguiente también es primo (los llamados “primos hermanos”). Sin embargo, hace un par de años, el hasta entonces desconocido matemático chino Yitang Zhang sorprendió al mundo académico al demostrar que, al menos, ¡hay infinitos primos que distan a lo más 70 millones de unidades del primo que les sigue! Rebajar ahora la distancia desde 70.000.000 a 2 parece una tarea abordable. De hecho, el proyecto en colaboración Polymath ya logró bajar la distancia inicial a 4.680. Sabemos entonces que hay infinitos primos que “ya no están tan solos”…

Otro problema de larga data (planteado por el húngaro Paul Erdös) fue resuelto la década pasada por Ben Green y Terence Tao, y constituyó el resultado clave para que a este último (muy probablemente, el matemático más brillante de la actualidad) le fuese otorgada la prestigiosa Medalla Fields el año 2006. Éste se trata de la existencia de cadenas de números primos arbitrariamente largas en las que la distancia entre uno y el que le sigue es siempre la misma. Si bien es un resultado puramente teórico (de hecho, estas cadenas de números debiesen en general comenzar con primos extraordinariamente grandes), su valor radica en lo profundo de su revelación: la secuencia de los números primos alterna largos momentos de gran caoticidad con lagunas en las que algún grado de estructura muy regular emerge. De cierta manera, esto concuerda con el hecho de que no existe ninguna fórmula matemática suficientemente “útil” que entregue todos los números primos.

Finalmente, no puede no mencionarse la solución a un problema planteado hace casi 300 años por Christian Goldbach: tras avances preliminares a principios del siglo XX del ruso Ivan Vinogradov y más recientemente de Terence Tao, Harald Helfgott logró probar que todo número impar puede ser escrito como la suma de no más de tres primos (vea http://www.elmostrador.cl/noticias/vida-en-linea/2015/09/08/matematico-peruano-resolvio-un-problema-de-271-anos-de-antiguedad/). Este notable resultado es aún más destacable por el hecho que Helfgott es de nacionalidad peruana y frecuente colaborador con matemáticos de nuestro país (vea por ejemplo http://www.sistemasdinamicos.cl/conferences/AGRA/webcontent_126.html Cabe señalar, sin embargo, que se desconoce aún si todo número par mayor que 2 puede ser escrito como la suma de dos números primos. Esta “conjetura de Golbach fuerte” parece estar aún lejos de ser resuelta.

Ciertamente, al margen de estos avances, sigue habiendo muchas pre-guntas relacionadas aparentemente muy sencillas. Por ejemplo, no se sabe si existen infinitos primos cuyo producto por 2 más 1 sea nuevamente un primo. Estos números, estudiados por primera vez por la matemática francesa Sophie Germain hace más de 200 años (y llamados “primos de Germain” en su honor), tienen hoy mucha importancia en criptografía.

Al igual que el firmamento, el universo de los números es un cosmos de gran belleza y complejidad, en el cual los primos “titilan (¿azules?) como astros a lo lejos”. Sin duda alguna, mientras la especie humana subsista, habrá quienes apunten sus telescopios imaginarios para seguir descubriendo uno a uno estos preciosos cuerpos y revelarnos sus secretos. A fin de cuentas, los números no dejan de ser una de las invenciones humanas más notables, y como tales nos acompañarán hasta nuestro último día.

*Andrés Navas

Presidente de la Sociedad Matemática de Chile