 Opinión
Opinión
La historia de estas estructuras se remonta a tiempos ancestrales. En efecto, usando membranas tejidas con fibras naturales, diversas comunidades desarrollaron construcciones basadas en la “tensión”. Sin embargo, y a pesar de la audacia con que llegaron a aplicar estas ideas, ninguna de ellas fue capaz de teorizarlas. Así, quien es considerado como precursor de las estructuras tensionadas es el arquitecto alemán Frei Otto. Curiosamente, sus primeras experiencias al respecto las tuvo en el campo de prisioneros en que estuvo recluido hacia fines de la Segunda Guerra Mundial, donde se encargó de la construcción de refugios tipo carpa.
El próximo miércoles, el Bayern de Múnich disputará la llave de ida de la semifinal de la Liga de Campeones. Es cierto: el fútbol europeo de clubes ha perdido en alguna medida su espíritu deportivo, convirtiéndose en una instancia de lucha entre unas pocas instituciones que acaparan gran parte de los recursos. A pesar de esto, este poderoso equipo, por el que han pasado leyendas del fútbol como Franz Beckenbauer, Sepp Maier, Gerd Müller, Karl-Heinz Rummenigge, Lothar Matthaus y Manuel Neuer, entre otros, sigue despertando aún la pasión de muchos aficionados. En algunos casos, esta viene reforzada por la espectacularidad del que fuera su estadio por más de treinta años, el Olímpico de Múnich. Y es que una hermosa y profunda teoría matemática, la de las superficies mínimas, es la secreta inspiración de la increíble cubierta que corona sus galerías.
De manera similar a nivel local, desde hace ya algunos años, muchos espacios públicos de nuestro país como terminales de pasajeros, pabellones de exposición, restaurantes y recintos de espectáculos, han sido cubiertos por membranas semitraslúcidas que, a simple vista, perecen simples carpas, pero que en realidad son muchísimo más sofisticadas. Estas operan siempre sobre la base del mismo principio: a grandes rasgos, sobre un esqueleto metálico rígido y sinuoso se extiende una membrana flexible, la cual es tensionada mediante cables de modo que alcance su forma “natural”. Así se origina una estructura que destaca no solo por su ligereza, eficiencia y economía, sino también por la elegancia de sus formas, muy alejadas de las clásicas pautas ortogonales de la arquitectura tradicional. De cierta manera, estas formas se adaptan al medio en lugar de imponerse a él, creando espacios que, además de unificados y correlacionados, son altamente sostenibles, sanos y diversos. Todo esto está muy acorde con una filosofía arquitectónica, el “organicismo”, la que, de manera aún más ambiciosa, promueve la armonía entre el hábitat humano y el mundo natural.

La historia de estas estructuras se remonta a tiempos ancestrales. En efecto, usando membranas tejidas con fibras naturales, diversas comunidades desarrollaron construcciones basadas en la “tensión”. Sin embargo, y a pesar de la audacia con que llegaron a aplicar estas ideas, ninguna de ellas fue capaz de teorizarlas. Así, quien es considerado como precursor de las estructuras tensionadas es el arquitecto alemán Frei Otto. Curiosamente, sus primeras experiencias al respecto las tuvo en el campo de prisioneros en que estuvo recluido hacia fines de la Segunda Guerra Mundial, donde se encargó de la construcción de refugios tipo carpa.
Más tarde, inició un proceso de investigación sistemático sobre estas técnicas, el que condujo a la fundación del Instituto para la Construcción de Estructuras Ligeras de la Universidad de Stuttgart. Hacia 1967, su diseño del Pabellón de Alemania Federal para la Exposición Universal de Montreal era una muestra de los inmensos avances ya alcanzados.

Sin embargo, encargarse de la cubierta del nuevo estadio que comenzaba a erigirse en Múnich era un desafío muchísimo mayor. Para lidiar con él, Frei Otto debió recurrir a conocimientos de vanguardia en matemática, a los cuales agregó una cuota de astucia sencillamente impresionante.
Para la matemática, una superficie es, someramente un objeto bidimensional sin puntas. Si la superficie logra conectar sus bordes usando la menor cantidad de material posible, es decir, si corresponde a la membrana de menor área que empalma a las mismas orillas, entonces es llamada mínima. Por ejemplo, un plano es la superficie mínima que llena un anillo, pero si cambiamos los bordes entonces aparecen formas diferentes. Entre las más sencillas figuran la catenoide (a izquierda), que corresponde a la membrana mínima que une dos anillos bien dispuestos uno en posición paralela a otro, y el helicoide (al centro), que es la superficie que traza una hélice al girar y simultáneamente subir a lo largo de un eje a velocidad constante. Un ejemplo más sofisticado es la superficie de Costa (a derecha), denominada así en honor a quien la descubrió en 1984, el matemático brasileño Celso José da Costa. Si quiere seguir disfrutando de tan sinuosas formas, puede acceder a un pequeño festival de superficies mínimas desde https://www.youtube.com/watch?v=vMls6jaRPwk.
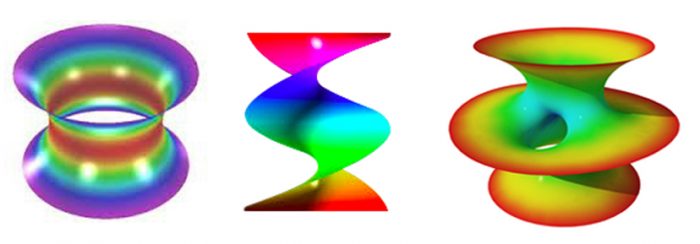
Naturalmente, son estas las formas que asume una estructura sometida a tensión, pues si el área de la membrana empleada no fuese mínima, entonces esta se podría tensionar aún más. El problema para su implementación como cubierta es que, dado que la forma está “curvada”, no puede ser reproducida mediante membranas planas. Más aún, ella se ajusta a complejas ecuaciones diferenciales, en torno a las cuales trató por ejemplo un importante trabajo del matemático estadounidense Jesse Douglas que le valió ser galardonado en 1936 con una de las primeras medallas Fields (un trabajo con los mismos resultados fue producido por el húngaro Tibor Radó, pero este, por razones de edad, ya no calificaba para el premio; vea http://www.elmostrador.cl/cultura/2016/03/17/fermat-wiles-y-el-nobel-de-la-matematica/). Y si bien hoy las soluciones a estas ecuaciones pueden ser muy bien aproximadas y bosquejadas con programas computacionales especialmente concebidos para esto (entre los que se encuentra rhinoceros 3D), hace cuarenta y cinco años eran difíciles de manipular.
Frei Otto se enfrentó a todos estos problemas para cubrir el coliseo de Múnich, y a ellos debió añadir aún uno más: dada la magnitud de su proyecto, este no podía consistir en envolver el estadio con carpas, sino en construir una cubierta de material más sólido cuya forma fuese exactamente igual al de una estructura tensada, de modo que pudiese soportar de la mejor manera posible las condiciones ambientales y, a su vez, presentara formas estéticamente llamativas.
Recordó entonces los experimentos del físico belga Joseph Plateau en el siglo XIX, quien trabajó con películas de jabón para obtener superficies mínimas. El proceso es muy sencillo: se toma uno o varios trozos de alambre de borde tan sinuoso como se quiera y luego se “cierran”, es decir, se unen sus puntos de inicio y final. Posteriormente, se los sumerge en una solución jabonosa y se los retira suavemente. Al sacarlos, la forma mínima y curvada en direcciones opuestas será automáticamente producida por la naturaleza (una presentación interactiva de este experimento aparece en https://www.youtube.com/watch?v=52wVrtA5krY).
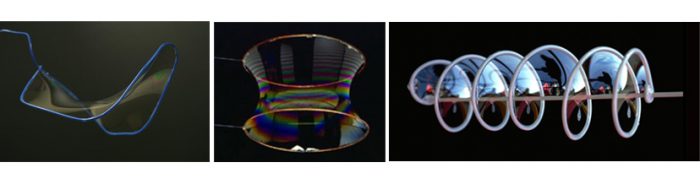
Fue usando este procedimiento que Frei Otto esbozó la cubierta del estadio de Múnich. Primeramente, construyó maquetas de lo que serían los soportes de las estructuras, y luego comenzó a experimentar, al igual que Plateau, con capas de burbujas que se acoplasen a ellas. La cubierta final fue, entonces, una reproducción a gran escala de este diseño burbujeante. Para su confección se usaron placas de poliéster de alta resistencia recubiertos con PVC. El resultado fue simplemente espectacular, y el mundo entero quedó maravillado el día de la inauguración de los Juegos Olímpicos de 1972 al contemplar el que hasta ese entonces era el estadio más moderno del planeta: https://www.youtube.com/watch?v=Lt7yeV1aTTc.
Frei Otto, uno de los arquitectos más influyentes del siglo XX, fue galardonado el año 2015 con el premio Pritzker (equivalente al Óscar en el área, el mismo que en 2016 fue otorgado al chileno Alejandro Aravena). Lamentablemente, su deceso se produjo solo días después de su nominación, convirtiéndose así su caso en el único premio póstumo de este tipo que ha sido conferido.
En cuanto al estadio, inició una lenta agonía hacia mediados de la década pasada: no fue sede del Mundial de Fútbol del 2006, y el propio Bayern se trasladó por esos años al Allianz Arena, donde se disputará la llave de vuelta de la semifinal del miércoles. Aun así, tanto el coliseo como toda la villa alrededor son un símbolo de la ciudad de Múnich: sus dependencias son utilizadas para conciertos y otras actividades, además de ser objeto de visitas guiadas (vea http://www.viajesfutboleros.com/como-disfrutar-del-olimpico-de-munich/). Recorrer estos parajes es un doble placer. Por un lado, están la arquitectura formidable y la sofisticada geometría que esconde. Por otro, la historia deportiva -en especial futbolística- que allí se guarda es de ensueño. Es como si se pudiese respirar el ambiente de aquella tarde de final de Mundial en 1974, en que una ordenada Alemania derrotó limpiamente a la temible Naranja Mecánica de Johan Cruyff:
http://www.dailymotion.com/video/x21dxz8_fifa-world-cup-1974-final-west-germany-vs-netherlands_sport. O de esa tarde de final de Eurocopa en 1988, en que el cuadro naranja se reivindicó gracias a un sublime gol de volea de Marco van Basten: https://www.youtube.com/watch?v=fkKK8H18tCA. Sin embargo, a pesar de tan recordadas gestas, el deleite de muchos será por siempre ese singular e irreverente partido entre filósofos ideado por el genial Monty Phyton: https://www.youtube.com/watch?v=ag7fK9y5iwk. Ciertamente, no podía haber un espacio más apropiado que el Estadio Olímpico de Múnich para recibir a dos equipos con tan selectas alineaciones…
