
Arte y matemática tienen una sincronía muchísimo más rica de la que se suele creer, la cual ha sido explorada a lo largo de la historia por diversas culturas. Esta interacción puede dar lugar aún a una infinitud de experimentaciones.
Antes de haber sido el título de una novela de D. Brown (el mismo autor de El Código Da Vinci), Ángeles y Demonios es el nombre de uno de los grabados mejor logrados del artista holandés M. Escher (1898-1972), famoso además por sus ilustraciones de paisajes imaginarios y figuras imposibles. Sin embargo, a menudo se ignora que detrás de esta obra perfecta que tan bien simboliza la dualidad humana se hallan profundos conceptos matemáticos, además de una inspiración en el arte arábico ancestral.

Escher era diseñador con estudios en arquitectura y realizó muchos viajes durante su juventud. A los 24 años visitó el palacio de la Alhambra en Granada, lo cual marcaría para siempre su carrera. Dicha construcción (declarada patrimonio de la humanidad por la UNESCO) es una de las más ornamentadas de la cultura árabe. En ella destacan en todo su esplendor los arabescos, diseños geométricos que decoran muros y techos de manera repetitiva. Dicho sea de paso, decoraciones de similares características fueron (y continúan siendo) producidas por innumerables culturas. Como ejemplo concreto y cercano, resulta interesante constatar las creaciones del pueblo diaguita, cuyo estudio debiera merecer mayor atención. Sin embargo, de entre todas, las decoraciones de la Alhambra destacan no sólo por su calidad técnica y estética, sino porque adelantan descubrimientos científicos de varios siglos posteriores.
Para explicar esto con un aire de cotidianeidad le sugiero mirar las paredes de su cocina o baño, alguna cortina o una prenda geométricamente decorada. Notará que muchas de ellas están tapizadas con modelos que se repiten con cierta frecuencia. En general, la repetición es horizontal y vertical, aunque también puede ser en una dirección inclinada. En algunos casos, el motivo y su disposición son tan regulares que se replican a sí mismos por rotaciones bien centradas, a veces en 180 grados, a veces en 90, otras en 60 y 120. Incluso pueden aparecer repeticiones del “tipo espejo” (llamadas reflexiones) frente a líneas bien escogidas. A todo este conjunto de simetrías y la forma en que ellas interactúan la matemática les denomina “grupo”, término no muy ilustrativo acuñado por el célebre E. Galois (el mismo que muriera a los 21 años en un duelo de caballeros tras una noche en la que escribió todos sus descubrimientos, previendo un desenlace fatal).
En 1891, el científico ruso E. Fedorov describió la lista de todos los grupos de repetición posibles, constatando la existencia de exactamente 17. Este resultado fue redescubierto por el matemático húngaro G. Pólya en 1924, quien en un artículo de investigación lo ilustró de una manera muy especial y con una nomenclatura no menos llamativa. Observe que cada decoración presenta elementos que la hacen intrínsecamente distinta a las otras. Por ejemplo, si bien la última admite rotaciones de 60 grados, la penúltima sólo admite rotaciones en 120 grados: los grupos subyacentes son, por lo tanto diferentes.
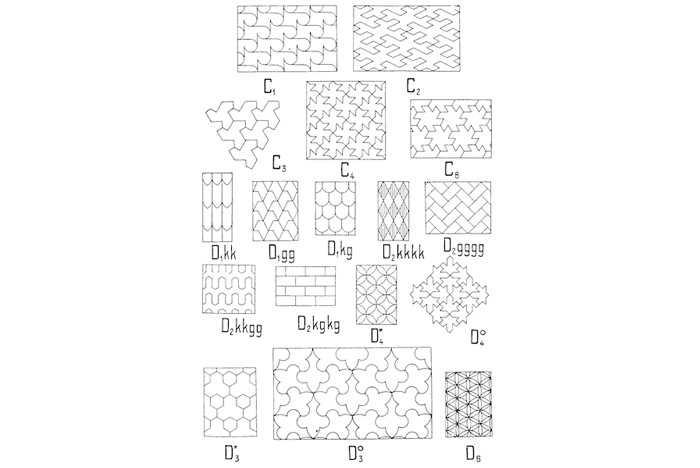
Sorprendentemente, las ornamentaciones de la Alhambra (cuya construcción se inició en el siglo XIII) replican estas 17 posibilidades, sin olvidar ninguna. Escher quedó maravillado ante todo esto e incorporó la idea de la repetitividad en su creación. Sin embargo, a diferencia del arte arabesco en el que, en general, cada figura decorativa tiene una posición bien diferencia-da del resto, en la obra de Escher las figuras se yuxtaponen en permanente competición unas con otras, en una rígida búsqueda del equilibrio. Pero tal vez la diferencia más importante radica en que Escher aprovechó todos los conocimientos matemáticos de su época. No en vano, usualmente señalaba que se hacía rodear más por científicos que por artistas. Es así como, tras conversaciones con el célebre geómetra canadiense H. Coxeter, incorporó un nuevo elemento a sus diseños, inimaginable esta vez para los antiguos decoradores: el de la geometría no euclidiana. Sin este toque, Ángeles y Demonios se vería así:

No es sino gracias a la geometría hiperbólica que la obra se ilustra en un disco en el cual las figuras se “deforman” hacia el borde. Escher comprendió a la perfección este efecto: tal deformación desaparece si “cambiamos nuestra forma de medir”: el mundo plano se reduce entonces a un disco cuyo borde es inalcanzable por estar a una distancia infinita. Curiosa y paradojalmente, el primer precursor de esta geometría fue un sacerdote, el jesuita G. Saccheri, quien sin embargo no logró desentrañarla pues estaba diabólicamente empecinado en probar su inexistencia… Hubo que esperar la genialidad de K. Gauss, J. Bolyai, N. Lobatschewski, B. Riemann, F. Klein y H. Poincaré para que sus misterios se revelaran, condensándose en uno de los inventos más notables del intelecto humano, cuya consagración máxima se dio quizás a través de las teorías de la relatividad de A. Einstein, en las que se aplica a la perfección.
Arte y matemática tienen una sincronía muchísimo más rica de la que se suele creer, la cual ha sido explorada a lo largo de la historia por diversas culturas. Esta interacción puede dar lugar aún a una infinitud de experimentaciones. Por ejemplo, incluso el arte erótico ha comenzado a apoderarse de la idea de repetitividad, como queda ilustrado en la obra Siluetas de Amor a la Luz de la Luna, del artista brasileño Fernando de la Rocque, la cual no deja de tener ciertas reminiscencias con las esculturas de Kahurajo en la India. Por simple deleite, se exhibe también una versión en geometría hiperbólica, obtenida a partir del original mediante un programa computacional ideado y gentilmente ejecutado para este artículo por el matemático, ingeniero y diseñador belga Jos Leys. Ciertamente, nuevas experimentaciones con esta técnica son aún posibles…


Arriba, Siluetas de Amor a la Luz de la Luna, de Fernando de la Rocque (*). Abajo, la misma obra modificada computacionalmente a la geometría hiperbólica por Jos Leys (**).
Andrés Navas
Dpto de Matemática y Ciencia de la Computación, USACH
Presidente de la Sociedad Matemática de Chile
*Siluetas de Amor a la Luz de la Luna, de Fernando de la Rocque http://fernandodelarocque.blogspot.cl
**Jos Leys http://www.josleys.com/