
 CULTURA
CULTURA
Para muchos la música es todo emoción, para otros, un rompecabezas matemático. Hemos usado las matemáticas para explicar la música durante siglos. Pitágoras dijo que los números gobernaban el universo. Pero se equivocó.
Podemos llamarlo humano, un instinto natural: nuestra especie está desesperada por entender y controlar la naturaleza, si no el universo entero. Y lo hacemos con los números.
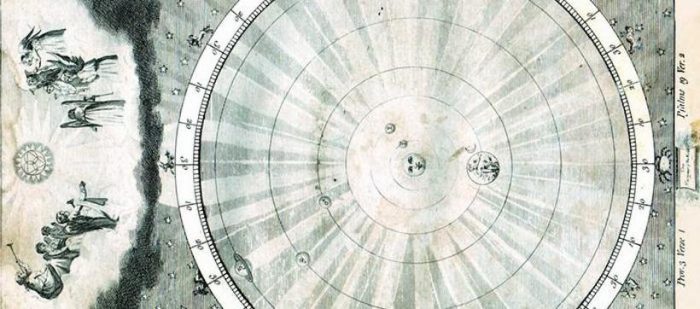
Los antiguos griegos fueron «verdaderos matemáticos», dice Eli Maor, un profesor jubilado de historia de las matemáticas y autor de Música por los números. Dirigidos en gran parte por Pitágoras, su lema, por así decirlo, era «los números gobiernan el universo». Miraban al cosmos como una «unidad de música, astronomía, geometría y teoría de los números, a la que llamaban aritmética», dice Maor. «La música se clasificaba como ciencia y la usaban para explicar las órbitas de los planetas y las estrellas».
Los pitagóricos eran un culto. Juraron mantener sus discusiones en secreto. Como resultado, poco o ningún registro escrito sobrevivió. Pero sabemos que Pitágoras experimentó con cuerdas vibratorias. Descubrió que si se divide una cuerda por una proporción de 2:1, 3:2 o 4:3, y pulsas la cuerda, como lo harías en una guitarra o violín, las notas resultantes tienen una «relación armoniosa». Están en consonancia.
«Y a partir de ahí, dio este enorme salto de fe para decir que todo el universo funcionaba según estos simples números», dice Maor.
Según él, la idea influyó en la ciencia «negativamente» durante miles de años, hasta que llegaron los astrónomos Johannes Kepler y Galileo Galilei.
Johannes Kepler fue la primera persona en entender los verdaderos movimientos de los planetas. Buscaba el movimiento perfecto. «Kepler era un pitagórico. Un verdadero creyente. Me atrevo a decir que 30 años de su corta vida fueron desperdiciados, buscando la órbita de los planetas en las leyes musicales de la armonía», dice Maor. «Finalmente, se dió cuenta de que la idea estaba equivocada.»
Eso no impidió que un grupo de científicos de la Universidad de Yale en la década de 1970, entre ellos Willie Ruff, un músico de jazz y musicólogo, convirtiera los inaceptables cálculos planetarios de Kepler en sonido utilizando la síntesis por computadora.
La teoría de la armonía universal de Pitágoras puede haber fallado, pero sus proporciones siguen vivas. Una proporción de 2:1 da una octava, dos de la misma nota, con un tono al doble de la frecuencia del otro. Una proporción de 3:2, mientras tanto, le da una quinta perfecta, desde la tónica hasta la nota superior de un acorde básico de tríada mayor.
El oído humano anhela tales estructuras familiares, sonidos que resuelvan, o «marcos de referencia», como explica Maor. Es la tonalidad la que nos da armonía; quizás más similar al sentido de armonía que Pitágoras buscaba en las estrellas.
La tonalidad ha sido un principio rector en la música desde el siglo XVII. La idea básica, y simplificada, es que la música está confinada a una cierta tonalidad y si se desvía, debe volver a la tonalidad original. No obstante, en el siglo XX, compositores como Arnold Schönberg comenzaron a pensar que la tonalidad había «completado su curso», dice Maor.
«Schönberg se propuso reemplazar la tonalidad con una forma de música atonal», dice Maor. «Me recuerda a la Teoría de la Relatividad de Einstein, porque los marcos de referencia son todos iguales».
Es una visión interesante, dado que Schönberg y Einstein eran contemporáneos. Se conocieron, al menos una vez, en un concierto en el Carnegie Hall en 1934. Fue una reunión de música y matemáticas, personificada. Pero ahí también puede ser donde termina la conexión. Los expertos de Schönberg le dirán que no hay leyes musicales en la música del compositor.
El serialismo, como se lo conoce a veces, tuvo origen en el dodecafonismo de Schönberg y evolucionó de varias maneras. Aplicaba reglas sobre la forma en que las notas de una escala se pueden colocar en una pieza, la forma en que aparecen en una serie y cómo forman un sentido de unidad en la música. Schönberg rechazó la repetición en una serie de notas o dictaminó que todas las notas deben tener el mismo valor, que no se puede enfatizar una sola nota más que otra.
Puede que no sean matemáticas, pero se le perdonaría a quien describa la técnica como matemática. El serialismo crea patrones basados en reglas que pueden conducir a una disonancia que nuestros oídos, o nuestra emoción, de lo contrario podrían rechazar, pero la teoría serial lo permite. Especialmente porque la falta de repetición significa que hay pocos marcos de referencia.
Más tarde, el teórico y filósofo musical, Theodor Adorno, sugirió que la «Neue Musik» (nueva música) de principios del siglo XX era algo más que el serialismo, o las reglas no armónicas. Se trataba de expresar sonidos que reflejaban el mundo que les rodeaba, que era cada vez más industrial y no armónico. Describir el universo tal como lo veían, en el arte. Lo que los pitagóricos esperaban hacer antes que ellos.
Otros siguieron a los serialistas. Steve Reich, Philip Glass, John Cage, Karlheinz Stockhausen y la musique concrète, ente muchos otros.
«La música es un intento de interactuar con cualquier entorno en el que te encuentres, para darle sentido, y como el entorno se ha vuelto cada vez más industrial y tecnológico, esa música ha pasado a primer plano en nuestro intento de entender nuestro entorno, de cómo estamos cambiando, y cómo la humanidad está evolucionando», dice Matt Black, músico y científico pionero del software creativo.
«Creo que todo es un equilibrio entre el orden y el caos», opina Black. «La onda sinusoidal (una suave oscilación periódica en el sonido) es un ejemplo de orden perfecto, es una señal completamente repetitiva, y aburrida porque puedes predecirla. El ruido blanco, por otro lado, es un completo caos. El caos está lleno de información, pero no tiene forma, y no es muy útil. Creo entonces que la vida y la conciencia existen en esa fase de transición entre el orden y el caos, en el punto de encuentro».
Demasiado orden es el estancamiento, dice Black, aburrido, nunca pasa nada interesante. Y cuando hay demasiado caos, nada tiene oportunidad de unirse u organizarse porque se hace pedazos.
Como sistemas, las matemáticas y la música son imperfectas. Pero a los matemáticos les gusta pensar que son puras, un sistema que hemos desarrollado para explicar, calcular y controlar la naturaleza. Pero si pudiéramos hacerlo completamente, «seríamos Dios», dice Black.
La música, por otro lado, permite cierta imperfección, la disonancia. No necesitamos entenderla o controlarla completamente. Podemos sentirla. Y tal vez por eso es que legiones de científicos de alto nivel tocan instrumentos, simplemente por amor a ella. Se dice que Albert Einstein tocaba el violín porque le ayudaba a pensar.
«Estamos obsesionados con el control de las cosas», dice Maor. «Creemos que cualquier fenómeno inusual debe tener alguna razón, y esa razón se basa en los números. Pero la música fue creada para mover nuestras almas, para tocar nuestros sentimientos, nuestras emociones. Y es por eso que la mayoría de los intentos de someter la música a las matemáticas han fracasado».