Lo de los panales de abejas ya había sido vislumbrado por Pappus de Alejandría en el siglo IV d. C.: las abejas “eligen” la más regular de estas configuraciones por ser la que minimiza el gasto de cera. De manera más precisa, cualquier otra que cubra la misma superficie y tenga igual número de celdas utilizará más cera. Darwin se refirió también a este fenómeno, señalando que esta “elección” de las abejas no era sino una confirmación de su teoría de la evolución.
Ya sea en la forma de los panales de las abejas, en las formaciones basálticas de la Calzada del Gigante en Irlanda o en los salares del altiplano andino, las configuraciones hexagonales están muy presentes en la naturaleza. Ello está lejos de ser una simple curiosidad, pues hay diversos procesos que condicionan este fenómeno. Lo de los panales de abejas ya había sido vislumbrado por Pappus de Alejandría en el siglo IV d. C.: las abejas “eligen” la más regular de estas configuraciones por ser la que minimiza el gasto de cera. De manera más precisa, cualquier otra que cubra la misma superficie y tenga igual número de celdas utilizará más cera. Darwin se refirió también a este fenómeno, señalando que esta “elección” de las abejas no era sino una confirmación de su teoría de la evolución.
Increíblemente, lo que para Pappus y Darwin era evidente (y estaba anclado en la vida de las abejas desde tiempos milenarios) no tuvo confirmación científica cabal hasta hace muy poco. Tras un avance fundamental en 1943 por el matemático húngaro L. Fejes Tóth, la prueba completa de la imbatibilidad de los hexágonos regulares fue dada recién en 1999 por T. Hales, de la Universidad de Pittsburgh.
[cita]Lo de los panales de abejas ya había sido vislumbrado por Pappus de Alejandría en el siglo IV d. C.: las abejas “eligen” la más regular de estas configuraciones por ser la que minimiza el gasto de cera. De manera más precisa, cualquier otra que cubra la misma superficie y tenga igual número de celdas utilizará más cera. Darwin se refirió también a este fenómeno, señalando que esta “elección” de las abejas no era sino una confirmación de su teoría de la evolución.[/cita]
Los procesos que determinan formaciones rocosas son más difíciles de explicar, pero en ellos también opera cierto “principio de minimalidad”. Sin embargo, si bien este principio funciona perfectamente en condiciones ideales, éstas no se dan en la naturaleza. Así es como en el salar de Uyuni en Bolivia pueden apreciarse variaciones en la forma de las regiones poligonales que aparecen, muchas de las cuales tienen, incluso, menos de seis lados. Curiosamente, es difícil hallar regiones con siete o más lados. Nuevamente, esto no es una casualidad. El ya desaparecido matemático I. Niven –de quien se conmemora este 25 de octubre el natalicio número 99– probó que es imposible cubrir el plano utilizando polígonos de más de seis lados, a menos que la disposición se vuelva eventualmente “degenerada”, es decir, que requiera polígonos cada vez más “alargados” y “achatados”.
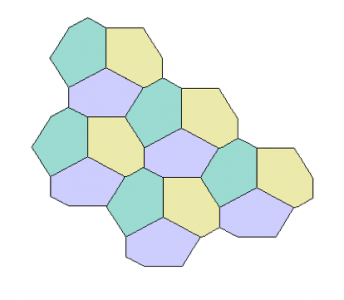
Como se observa más abajo, existen otras configuraciones que permiten cubrir el plano utilizando un único patrón hexagonal no regular dispuesto de manera astuta. De hecho, todas las diferentes posibilidades fueron descritas por K. Reinhardt en su tesis doctoral de 1918, bajo la dirección del célebre matemático D. Hilbert. Hace unos meses intenté leer este trabajo con pésimos resultados: además de su larga extensión, está escrito en un alemán no muy moderno, y la terminología empleada no es en absoluto convencional. Decidí entonces pedir ayuda a los especialistas del tema, y la respuesta que recibí de uno de ellos –Branko Grünbaum– me dejó aún más perplejo: “Tanto la tesis de Reinhardt como trabajos posteriores en este tema específico son tremendamente complicados, y muy probablemente incompletos; sería muy útil retomarlos hasta obtener una simplificación que sea digerible”. Entiéndase bien: nadie en el mundo es capaz de reproducir los argumentos de este trabajo, ¡pero la comunidad matemática concuerda en que estos son correctos! Aunque suene extraño, este tipo de situaciones suele ocurrir en esta ciencia.
 En fin, mientras nadamos en este tormentoso mar de dudas, desde el fondo seguirán emergiendo los hexágonos, con una leve sensación de triunfo… Y si este tipo de divagaciones no le estimula no importa: de todas formas, continuará viendo hexágonos en su diario vivir por bastante tiempo, ya sea en muchas construcciones, enrejados u ornamentaciones. Para comenzar a convencerse, tan sólo mire atentamente esta fotografía (le será familiar):
En fin, mientras nadamos en este tormentoso mar de dudas, desde el fondo seguirán emergiendo los hexágonos, con una leve sensación de triunfo… Y si este tipo de divagaciones no le estimula no importa: de todas formas, continuará viendo hexágonos en su diario vivir por bastante tiempo, ya sea en muchas construcciones, enrejados u ornamentaciones. Para comenzar a convencerse, tan sólo mire atentamente esta fotografía (le será familiar):
